AVL TREE

AVL TREE & B- Tree

AVL TREE
AVL Tree merupakan subtype dari Binary Search Tree. AVL sendiri merupakan kepanjangan dari nama pembuat dari konsep AVL Tree ini, yaitu Adelson,Velskii dan Landis. Singkatnya,AVL Tree merupakan dynamic self balancing Binary Search Tree.AVL Tree dijamin memiliki perbedaan dalam subtree kanan dan subtree kiri antara 1,0, atau -1. Adanya AVL Tree ini mempercepat searching algorithm dari BST sendiri dengan waktu O(log n). Dalam AVL Tree ini terdapat beberapa kasus yaitu:

LEFT LEFT CASE:
left - left case ini terjadi apabila terjadi ketidakseimbangan di sebelah kiri child dari subtree kiri sehingga lakukan right rotation.

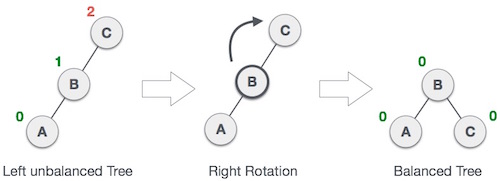Contoh LEFT LEFT Case dengan right rotation.

LEFT RIGHT CASE:
Left - right case ini terjadi apabila terjadi ketidakseimbangan di sebelah kanan child dari subtree kiri sehingga lakukan left rotation, lalu right rotation.

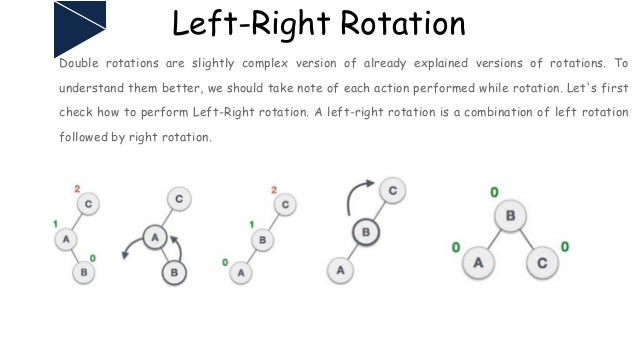Contoh Left Right rotation sehingga rotate kiri terlebih dahulu lalu rotate kanan.

RIGHT RIGHT CASE:
Right - right case ini terjadi apabila terjadi ketidakseimbangan di sebelah kanan child dari subtree kanan sehingga lakukan left rotation

Contoh RIGHT RIGHT CASE dengan melakukan left rotation

RIGHT LEFT CASE:
Right - Left case ini terjadi apabila terjadi ketidakseimbangan di sebelah kiri child dari subtree kanan sehingga lakukan right rotation terlebih dahulu, baru left rotation.

Contoh Right Left Case dengan melakukan right Rotation terlebih dahulu, lalu left rotation.

Berikut coding dari AVL Tree
#include<stdio.h>
#include<stdlib.h>
typedef struct Node{
int value;
struct Node *right,*left;
int ht;
}Node;
Node *createNewNode(int value);
Node *insertNode(Node *root,int value);
Node *rotateRight(Node *x);
Node *rotateLeft(Node *x);
Node *RR(Node *root);
Node *LL(Node *root);
Node *LR(Node *root);
Node *RL (Node *root);
Node findMax(Node *root);
int BF(Node *root);
int getHeight(Node *root);
int main()
{
Node *root = NULL;
root = insertNode(root,30);
root = insertNode(root,10);
root = insertNode(root,25);
}
Node *createNewNode(int value)
{
Node *temp = (Node *) malloc(sizeof(Node));
temp->value = value;
temp->left = temp->right = NULL;
temp->ht = 0;
return temp;
}
void *deleteNode(Node *root,int value)
{
if(!root)
return;
if(root->value < value)
root->right = deleteNode(root->right, value);
else if(root->value > value)
root->left = deleteNode(root->left,value);
else{
// no child
if(!root->right && !root->left)
{
free(root);
root = NULL;
}
else if(!root->right)
{
Node *temp = root;
root = root->right;
free(temp);
}
else if(!root->left)
{
Node *temp = root;
root = root->left;
free(temp);
}
//2 child
else{
Node *temp = findMax(root->left);
root->value = temp->value;
root->left = deleteNode(root->left,temp->value);
}

int BFactor = BF(root);
printf("BF = %d\n",BFactor);
//Left - Left Case
if(BFactor > 1 && root->left->value > value)
{
root = LL(root);
}
//Left- Right Case
else if(BFactor > 1 && root->left->value < value)
{
root = LR(root);
}
// Right - Right Case
else if(BFactor < -1 && root->right->value < value)
{
root = RR(root);
}
//Right- Left Case
else if(BFactor < -1 && root->right->value > value){
root = RL(root);
}
return root;
}

}
Node *findMax(Node *root)
{
if(!root->right)
return;
return findMax(root->right);
}
Node *insertNode(Node *root,int value)
{
if(!root)
return createNewNode(value);
else if(root->value > value)
root->left = insertNode(root->left,value);
else if(root->value < value)
root->right = insertNode(root->right,value);
//Update height
root->ht = getHeight(root);
printf("%d",root->ht);
//Case
int BFactor = BF(root);
printf("BF = %d\n",BFactor);
//Left - Left Case
if(BFactor > 1 && root->left->value > value)
{
root = LL(root);
}
//Left- Right Case
else if(BFactor > 1 && root->left->value < value)
{
root = LR(root);
}
// Right - Right Case
else if(BFactor < -1 && root->right->value < value)
{
root = RR(root);
}
//Right- Left Case
else if(BFactor < -1 && root->right->value > value){
root = RL(root);
}
return root;
}
Node *rotateRight(Node *x)
{
Node *y = x->left;
x->left = y->right;
y->right = x;
//Update height
x->ht = getHeight(x);
y->ht = getHeight(y);
return y;
}
Node *rotateLeft(Node *x)
{
Node *y = x->right;
x->right = y->left;
y->left = x;
//Update Height
x->ht = getHeight(x);
y->ht = getHeight(y);
return y;
}
Node *RR(Node *root)
{
return rotateLeft(root);
}
Node *LL(Node *root)
{
return rotateRight(root);
}
Node *LR(Node *root)
{
root->left = rotateLeft(root->left);
return rotateRight(root);
}
Node *RL (Node *root)
{

root->right = rotateRight(root->right);
return rotateLeft(root);
}

int BF(Node *root) // balanceFactor
{
int lh = 0,rh = 0;
if(root->left != NULL){
lh = root->left->ht + 1;
}
if(root->right != NULL){
rh = root->right ->ht + 1;
}
return lh - rh;
}
int getHeight(Node *root)
{
if(!root)
return -1;
return 1 + (getHeight(root->left) > getHeight(root->right) ? getHeight(root->left) : getHeight(root->right));
}