Binary Search Tree
Binary Search Tree
Binary Search Tree (BST) merupakan sebuah struktur data yang digunakan untuk menyimpan suatu barang (seperti angka,nama dan lain lainnya) dalam suatu memori. Binary Search Tree menyimpan kunci mereka secara tersortir.Disebut Binary Tree karena setiap tree nya memiliki maximum 2 anak / child dan disebut search tree karena dapat mencari suatu angka dalam waktu O(Log (n)).Yang membedakan dari Binary Search tree dan Binary Tree adalah,sebelah kiri sub tree dari suatu node harus lebih kecil dari node tersebut.Dan sebelah kanan sub tree dari suatu node harus lebih besar dari node tersebut.Terdapat operasi basic dari Binary Search Tree yaitu :
a).Insert
Memasukan sebuah data ke dalam BST.Apabila suatu data lebih kecil dari node data/key nya,maka melakukan pengecekan secara berulang.Sedangkan apabila suatu data lebih besar dari node data/key nya maka akan melakukan suatu pengecekan secara berulang.Ulangi sampai menemukan node yang kosong untuk dimasukan oleh data tersebut.
 |
| Contoh Insert pada BST.sumber :https://www.techiedelight.com/wp-content/uploads/Insert-into-BST.png |
b).Search
Mencari suatu data dalam BST.Apabila data root itu yang dicari,maka berhenti.Apabila data yang dicari lebih besar dari root maka lakukan pengecekan ke arah kanan secara rekursif.Sedangkan apabila yang dicari lebih kecil dari root maka lakukan pengecekan ke arah kiri.
 |
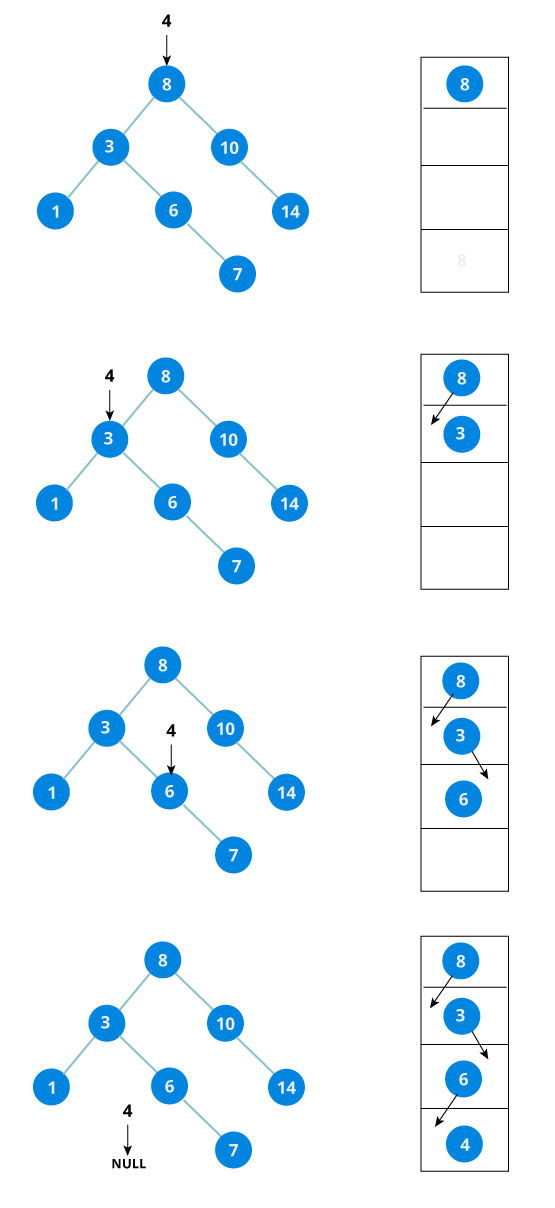| Contoh Search pada Binary Search Tree.Sumber:https://cdn.programiz.com/sites/tutorial2program/files/bst-downward-recursion-step.jpg |
c).Delete
Terdapat 3 kasus yang perlu dipikirkan yaitu:
-Menghilangkan suatu node tanpa memiliki child : langsung menghapus node tersebut.
-Menghilangkan suatu node dengan memiliki satu child/anak : Menghapus node tersebut dan menggantinya dengan child/anak tersebut.
-Menghilangkan suatu node dengan memiliki dua anak/child : Menghapus node tersebut dan menggantinya dengan child/anak tsb.Dapat menggunakan 2 cara untuk mengganti nya yaitu dengan mencari sub-tree ke kiri child paling kanan (leafnya) atau dengan mencari sub tree ke kanan child paling kiri(leafnya)
 |
| Contoh Delete pada Binary Search Tree.Sumber :https://blogger.googleusercontent.com/img/proxy/AVvXsEhDJmIW3iCO9q1ruSIBPADvauR_8L0AZG8UCS7XBk6wFvm3lAU6Tk0yZ_mk3aHGRGJogeym3tXr2JbUt3cYUPOIA0pCTNYZjRn9MHixlWx3aPfARdErWkYWxObl1NJMgt3-dhQU4ywb2V8GDvhiFNkStetaqq0F2j-frEX6gcKxsPbfOP6mwfDIVMV36Q= |
Sumber :
https://www.youtube.com/watch?v=mtvbVLK5xDQ -Binary Search Tree in Animated Demo
Berikut contoh Operasi BST(Binary Search Tree) pada C :
#include<stdio.h>
#include<stdlib.h>
typedef struct SinglyLinkedList{
int data;
struct SinglyLinkedList *left,*right;
}SinglyLinkedList;
SinglyLinkedList *createNewNode(int data){
SinglyLinkedList *temp = (SinglyLinkedList *) malloc(sizeof(SinglyLinkedList));
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
SinglyLinkedList *insert(SinglyLinkedList *root,int data){
if(root == NULL){
root = createNewNode(data);
}
else if(data < root->data)
root->left = insert(root->left,data);
else
root->right = insert(root->right,data);
return root;
}
int search(SinglyLinkedList *root,int data){
if(root == NULL){
return -1; // artinya tidak ada di dalam tree
}
if(root->data == data){
return 0; //artinya ada di dalam tree
}
else if(root->data < data){
return search(root->right,data);
}
else
return search(root->left,data);
}
SinglyLinkedList *findMinimum(SinglyLinkedList *curr)
{
if(curr->left == NULL)
return curr;
return findMinimum(curr->left);
}
SinglyLinkedList * deleteNode(SinglyLinkedList *root,int data){
if(root == NULL)
return root;
else if(root->data < data)
root->right = deleteNode(root->right,data);
else if(root->data > data)
root->left = deleteNode(root->left,data);
else{
if(root->left == NULL && root->right == NULL)
{
root = NULL;
}
else if(root->left == NULL){
root = root->right;
}
else if(root->right == NULL){
root = root->left;
}
else{
SinglyLinkedList *temp = findMinimum(root->right);
root->data = temp->data;
root->right = deleteNode(root->right,temp->data);
}
}
return root;
}
void printInorder(SinglyLinkedList *root)
{
if(root == NULL)
return;
printInorder(root->left);
printf("%d ",root->data);
printInorder(root->right);
}
int main (){
int x;
SinglyLinkedList *root = NULL;
root = insert(root,7);
root =insert(root,8);
root = insert(root,10);
root = insert(root,3);
root = insert(root,90);
if(search(root,30) == 0)
printf("True\n");
else
printf("False\n");
//false karena tidak ada 30 di dalam tree.
printInorder(root); //menggunakan inorder untuk print tree.
printf("\n");
root = deleteNode(root,10); //delete Node
printInorder(root); //menggunakan inorder untuk print tree.
printf("\n");
}
Comments
Post a Comment