Hash Tables and Trees

Hashing,Hash Tables,Trees and Binary Tree

Hashing

Hashing merupakan tehnik untuk menyimpan dan mengambil kunci dengan cepat.Hashing mengubah panjang input ke string dengan ukuran tetap.Artinya,seberapa banyak panjang input yang diberikan,dapat diubah menjadi array dari string dan angka melalui suatu algoritma.Pesan yang akan di hashing adalah input,algoritma yang akan digunakan untuk hashing disebut hash function dan hasilnya disebut hash value.

Hash Tables

Hash tables adalah suatu table / array  dimana tempat menyimpan string yang original.Ukuran hash table biasanya lebih sedikit dari jumlah string yang mungkin sehingga beberapa string memiliki hashed key yang sama.

Hash Function
Ada banyak cara untuk mengubah suatu string ke key,yaitu bisa dengan :
a).Mid - square :  Mengkuadratkan suatu string,lalu gunakan digit tengah sebagai hash key.Seperti contohnya nilai = 3121. Di kuadratkan menjadi 9740641 lalu diambil digit tengah yaitu 406 sebagai hash keynya.
b).Division : Membagi suatu string menggunakan operator modul.Seperti contohnya : "HELLO" akan di masukan di lokasi (64+8+64+5+64+10+64+10+64+15) % 97 = 77
c).Folding : Mempartisi string ke beberapa bagian,lalu tambahkan partnya untuk mendapatkan hash keynya.Seperti contohnya 123.Membagi menjadi 1 dan 23 sehingga hash keynya menjadi 24.(anggap lokasi ada 50).Apabila melebihi 50, seperti contohnya 56,biarkan angka awalannya sehingga menjadi 6.
d).Digit Extraction : Digit yang telah ditentukan dari yang diberikan akan dijadikan alamat hash.Seperti contohnya 123456. Apabila mengambil di bagian ke 2 ,ke 3 dan ke 4, akan mendapatkan 234 sehingga hash key nya adalah 234.
e).Rotating Hash : Menggunakan cara hash apapun seperti division atau mid-square.Setelah mendapatkan hash code dari cara hash tersebut,lakukan rotasi.Dimana rotasi dilakukan dengan men-shift kan dikit menjadi alamat hash.Seperti contohnya 123456,dengan rotasi ,akan didapatkan menjadi 654321 sebagai alamat hash yang baru.

Collision : Collision terjadi ketika 2 data yang memiliki hash value yang sama.Untuk itu,terdapat 2 cara untuk menangani collision yaitu dengan cara :
a).Linear Probing
Dilakukan dengan cara mencari slot yang kosong dan memasukan string tersebut disana.

Contoh Linear probing.Sumber :https://www.mathcs.emory.edu/~cheung/Courses/323/Syllabus/Map/FIGS/map44b.gif

b).Chaining
Memasukan string di slot sebagai linked list.

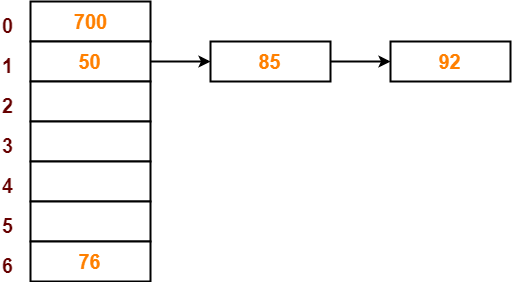Contoh Chaining.Sumber:https://media.geeksforgeeks.org/wp-content/cdn-uploads/gq/2015/07/hashChaining1.png

Implementasi Hash Table dengan Separate Chaining di C sebagai berikut :
#include<stdio.h>
#include<stdlib.h>
#define SIZE 10
typedef struct linkedList{
int data;
struct linkedList *next;
}linkedList;
linkedList *head[SIZE] = {NULL};
int hashKey(int x)
{
return x % SIZE;
}
void insert(int data,int hashedKey){
linkedList *temp = (linkedList *) malloc(sizeof(linkedList));
linkedList *temporary = head[hashedKey]; // input data
temp->data = data;
if(head[hashedKey] == NULL)
{
head[hashedKey] = temp;
head[hashedKey]->next = NULL;
}
else{
if(temporary->data == data){
printf("Data already in list\n");
return;
}
while(temporary->next != NULL){
if(temporary->data == data){
printf("Data already in list\n");
return;
}
temporary = temporary->next;
}
temporary->next = temp;
temp->next = NULL;
}
printf("--Input Successfully--\n");
}
void printHash(){
for(int i = 0 ; i < SIZE ; i ++){
linkedList *temp = head[i];
printf("Indexes at %d : ",i);
if(temp == NULL){
printf("No Entry\n");
}
else{
while(temp != NULL){
if(temp->next == NULL)
printf("%d \n",temp->data);
else
printf("%d->",temp->data);
temp= temp->next;
}
}
}
}
void searchHash(int data,int hashedKey)
{
linkedList *temp = head[hashedKey];
while(temp != NULL){
if(temp->data == data)
{
printf("Search element is found !\n");
return;
}
}
printf("Search element is not found\n");
}
void deleteHash(int data,int hashedKey)
{
if(head[hashedKey] == NULL){
printf("Data is not in the list !\n");
return;
}
linkedList *temp = head[hashedKey];
if(head[hashedKey]->data == data){
head[hashedKey] = temp->next;
free(temp);
return;
}
else{
while(temp->next->data != data && temp->next != NULL)
temp = temp->next;
if(temp->next == NULL){
printf("Data is not in the list !\n");
return;
}
linkedList *temp1 = temp->next;
temp->next = temp1->next;
free(temp1);
}
}
int main ()
{
int x;
int item;
int hashedKey;
do{
printf("1.Add Item\n");
printf("2.Search Item\n");
printf("3.Remove Item\n");
printf("4.Show Item\n");
printf("5.Exit\n");
do{
scanf("%d",&x);
}while(x < 1 || x > 5);
switch(x){
case 1:
printf(">>Input data to insert[Integer]: ");
scanf("%d",&item);
hashedKey = hashKey(item);
insert(item,hashedKey);
break;
case 2:
printf(">>Input data to search[Integer]: ");
scanf("%d",&item);
hashedKey = hashKey(item);
searchHash(item,hashedKey);
break;
case 3:
printf(">>Input data to remove [Integer]: ");
scanf("%d",&item);
hashedKey = hashKey(item);
deleteHash(item,hashedKey);
break;
case 4:
printHash();
break;
}
}while(1);
}

Trees
Trees merupakan non linear struktur data yang merepresentasikan hirarki hubungan antar objek data.Node di dalam tree dapat dimasukan dimana saja dan terhubung dengan pointer.Sebuah tree dapat di definisikan secara rekursif sebagai koleksi node yang di mulai di akar node/root node dimana setiap node mengandung suatu value bersama dengan merujuk ke node lainnya.
Konsep Tree

a).Root = Node paling atas
b).Edge = garis yang menghubungkan parent ke child
c).Leaf = Node yang tidak memiliki child
d).Degree of node = Degree suatu node adalah total sub-tree pada node
e).Sibling = Node yang memiliki parent yang sama
f).Height/Depth = maksimum degree pada suatu node
g).Ancestor & Descendant = Jika terdapat garis yang menghubungkan node p ke node q,maka p disebut ancestor dan q adalah descendant dari p.

Binary Tree
Binary tree merupakan tree yang memiliki dua child di setiap nodenya(child kiri & child kanan).
Terdapat tipe Binary tree yaitu :
a).Perfect Binary Tree = binary tree yang setiap levelnya memiliki kedalaman yang sama.
b).Complete Binary Tree =binary tree yang setiap levelnya kecuali yang kemungkinan terakhir,terisi dan setiap nodenya paling panjang ke kiri.Perfect Binary Tree termasuk dengan Complete Binary Tree.

c).Skewed Binary Tree = binary tree yang memiliki setiap node paling banyak 1 child.

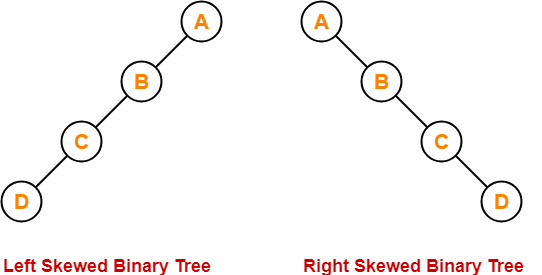sumber :https://www.gatevidyalay.com/wp-content/uploads/2018/07/Skewed-Binary-Tree-Example.png

d).Balanced Binary Tree = binary tree yang dimana tidak ada leaf yang paling jauh dari root dibanding leaf lainnya.

sumber :https://www.baeldung.com/wp-content/uploads/2019/11/Zrzut-ekranu-2019-10-31-o-15.31.40.png

Sumber :
https://www.tutorialspoint.com/data_structures_algorithms/hash_data_structure.htm
https://en.wikipedia.org/wiki/Hash_table
https://www.youtube.com/watch?v=shs0KM3wKv8 - Data Structure: Hash Table
https://en.wikipedia.org/wiki/Tree_(data_structure)
https://www.youtube.com/watch?v=qH6yxkw0u78 - Data Structures: Introduction to Trees